Introduction

This post was written with Richard Y. Liu. I thank Alison Wendlandt, Hayden Sharma, Dennis Kutateladze, Corin Wagen, and Rob Knowles for some very interesting discussions.

In a remarkable pre-print, Knowles and co-workers have reported a catalytic deracemization reaction driven by light. In simplified form:

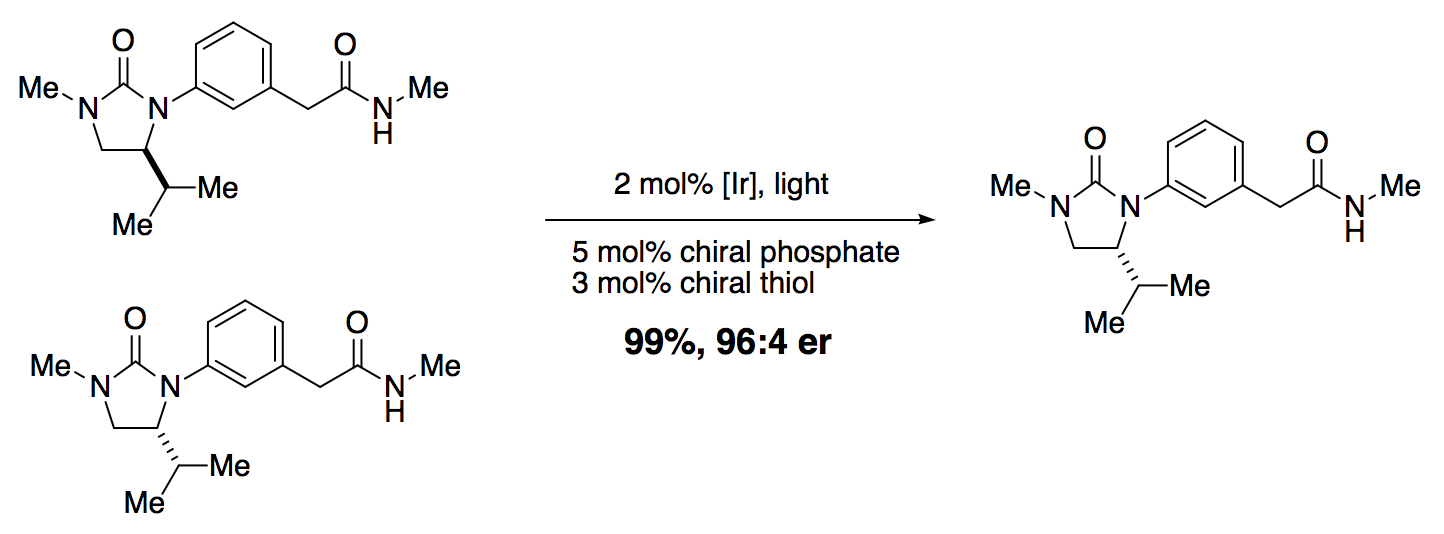
Catalytic deracemization is difficult for two reasons:

• Thermodynamics: the free energy of the racemate is lower than the free energy of the pure enantiomer. That is, even though a single molecule of R enantiomer is the same energy as a single molecule of S enantiomer, a racemic ensemble of R and S molecules is lower in energy than an enantiopure ensemble. (This distinction between potential energy and free energy can sometimes be a source of some confusion.)

• Kinetics: microscopic reversibility. If the catalyst makes a pathway from R to S accessible, it must also make a pathway from S to R to accessible.

Typical catalytic enantioselective reactions do not face these problems because the products are lower in both potential and free energy than the starting materials. In catalytic deracemization reactions, it is necessary to couple the deracemization process, which is necessarily neutral in potential energy and uphill in free energy, to a downhill process. Previous efforts have accomplished this by coupling to chemical redox or photochemical energy transfer.

In the Knowles study, light was used to drive continuously the system away from equilibrium. While a stereoselective ablation process preferentially destroys one enantiomer, a stereoselective regeneration process continuously favors the formation of the other enantiomer. Below, we examine the kinetics behind this process and consider the question of how ablation and regeneration work together to achieve high enantioselectivity.

The Mechanism

How does the transformation work? Starting from one enantiomer of substrate:

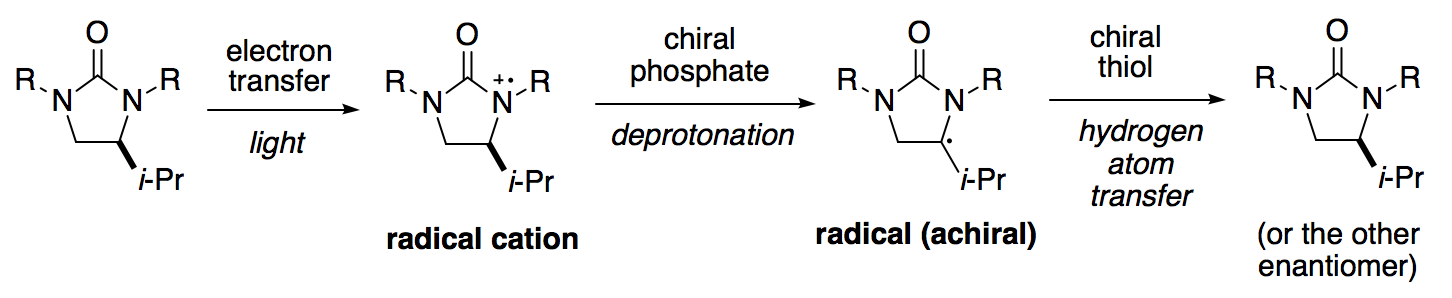
• Electron transfer: Photoexcitation of an iridium catalyst produces an oxidant, which removes an electron from the substrate. Presumably, both substrate enantiomers are oxidized at the same rate by the racemic oxidant.

• Proton transfer: Electron transfer generates a radical cation, which can be deprotonated by a phosphate catalyst. By using a chiral phosphate, one enantiomer of radical cation can be deprotonated faster than the other to generate an achiral carbon-centered radical. Overall, this means that one enantiomer of substrate can be destroyed, or “ablated,” faster than the other.

• Hydrogen atom transfer: The substrate can be regenerated by transfering a hydrogen atom to the radical. By using a chiral thiol, transfer can occur more quickly on one prochiral face, leading to the preferential regeneration of one substrate enantiomer.

The Kinetics

The kinetic scheme is:

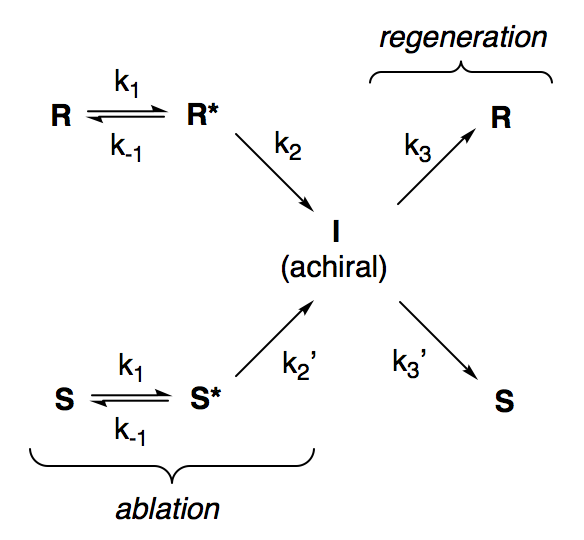
where:

• R and S represent enantiomers of the substrate in their ground state
• R* and S* represent enantiomers of the substrate as their radical cations
• I represents the achiral carbon-centered radical

Presumably, R and S are the only observable substrate species in this reaction, meaning that R*, S*, and I are reactive intermediates that are being formed and destroyed at equal rates. Applying this steady-state approximation to R:

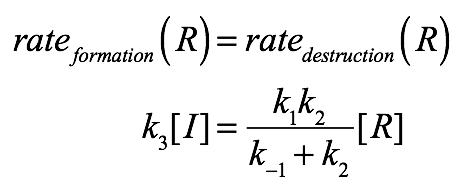
The left-hand-side is simply the first-order rate for generating R from I. The right-hand-side considers the R to R* to I sequence as a unit. That is, R is destroyed by becoming I, and the rate for this is given by the Michaelis-Menten equation.

Similarly, for S, we have:

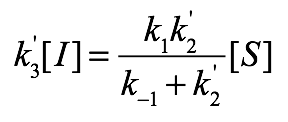
We can then divide these two equations to determine the steady state ratio of R to S:

The first term represents stereoselective ablation, while the second term reflects stereoselective regeneration. We can then consider two scenarios:

Back-electron-transfer is Fast

• Under these conditions, the electron transfer step is reversible, such that deprotonation determines which enantiomer of substrate is preferentially ablated. Since both the ablation and regeneration steps are stereoselective and independent, both selectivities multiply to give the overall selectivity:

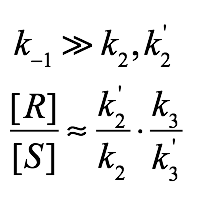
• Note that the enantioselectivity ratios are reversed, in that the abalation selectivity is given as a preference for S destruction, while the regeneration selectivity is given as a preference for R creation. This makes sense, given that preferentially destroying S while preferentially creating R will lead to enrichment of R.

• The potential energy diagram is:

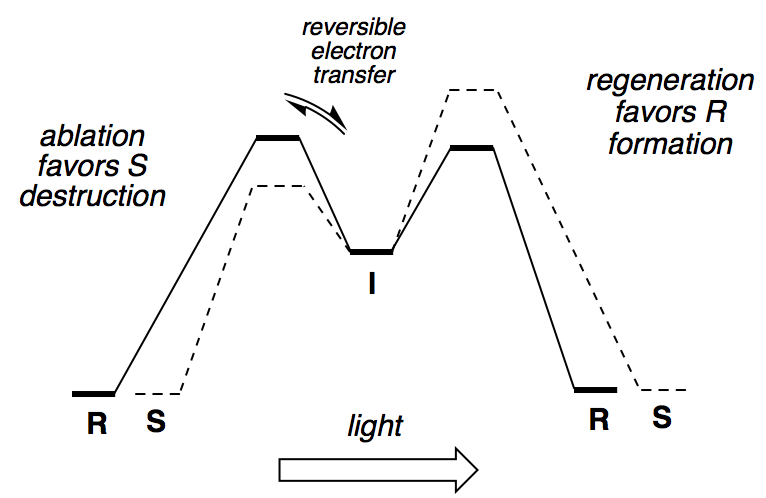
Note that the barrier for going forwards from I is higher than the barrier for going backwards from I, meaning that electron transfer is reversible.

Back-electron-transfer is Slow

• In this case, electron transfer is irreversible, such that both enantiomers off substrate are ablated at the same rate. Since only the regeneration phase is selective, the overall selectivity is:

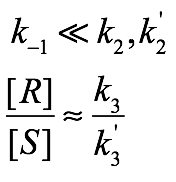
• The potential energy diagram is:

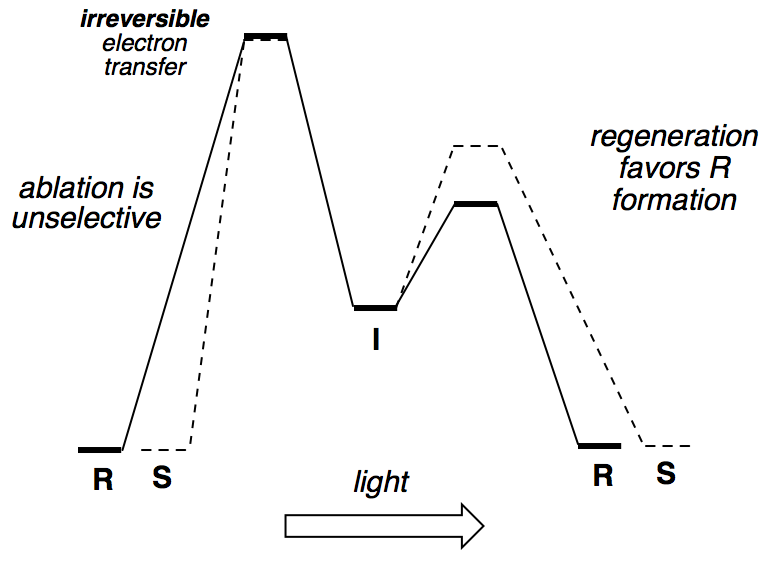
Note that the barrier for going forwards from I is now lower than the barrier for going backwards from I, meaning that electron transfer is irreversible.

Conclusion

The authors measured the enantioselectivity in this system with a chiral phosphate and an achiral thiol, as well as an achiral phosphate and chiral thiol. If the proposed mechanism is operative, the selectivities observed in these experiments reflects the intrinsic selectivities of ablation and regeneration. Furthermore, the fact that these intrinsic selectivities do, in fact, multiply to give the observed selectivity when both a chiral phosphate and a chiral thiol are used, indicates that back-electron-transfer is fast, and strongly supports the model proposed by the authors.

This is remarkable work. By engineering a system in which stereoablation and regeneration are under the independent control of two different catalysts, the overall selectivity is multiplicative. This “independent catalysis” situation is not only very rare in asymmetric catalysis, but extremely desirable. This is because the optimal catalyst for one fundamental step may be very different from the optimal catalyst for another step. Furthermore, it seems likely that the strategy described here will be applicable to other systems. For example, in more complex systems, where the intermediate carbon-centered radical may only be locally achiral, an analgous pseudoablation/regeneration approach should also result in deracemization. As further applications of this concept to other systems emerge, the implications for asymmetric catalysis will likely be profound.